Examples of our research activities
Dynamical structures of life
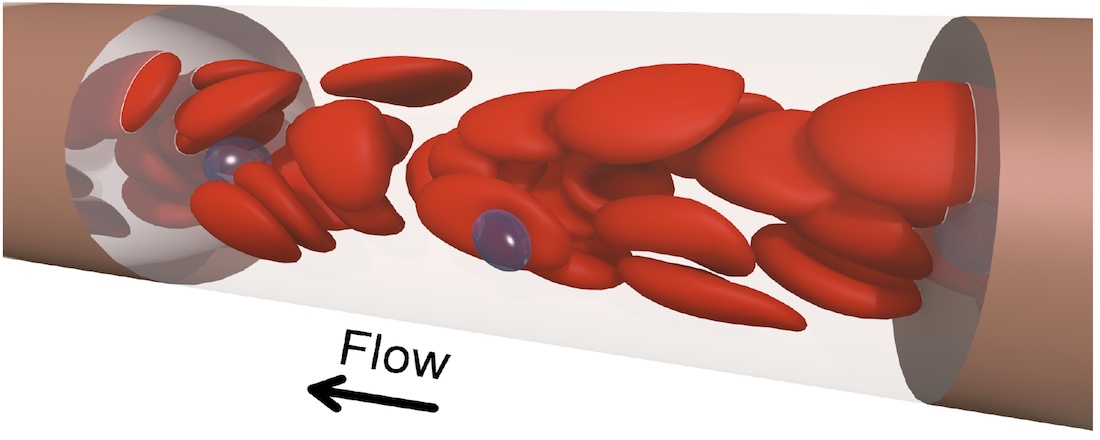
Living systems lead to the creation of complex spatial structures. The formation of organisms from egg cells (Weiss), the engulfment of particles by cells (Kress), the flow behavior of red blood cells (Gekle), the motility and self-organization of microbial communities (Bäumchen) or biogeography (Beierkuhnlein) and biodiversity (Jentsch) are but a few examples. In a linear world these phenomena would not be possible. Nonlinearities are a prerequisite for life.
Turbulence
Turbulent flows are abundant in our everyday life. They influence our daily weather (Thomas) as well as our long-term climate (Aizinger). Understanding turbulence in plasmas and around wind turbines is furthermore essential for future energy supplies or astro physics (Peeters). The combination of statistical theories and simulation (Wilczek) promises to offer new insights into this complex phenomenon.
Networks and artificial intelligence
Interconnecting a large number of simple, but independent units can lead to the creation of systems with novel, complex and nonlinear behavior. This applies to networks of magnetic particles (Fischer) or single molecules (Weber) equally well as to polymer networks (W. Köhler) or actively swimming particles (Schmidt). Complex networks are furthermore an important building block of socio-economical systems such as infection models (Chudej) or supply chains (Rambau). Neural networks as they appear in the brain of animals (Schuster) form the basis for artificial intelligence, e.g. in computer-based medical applications (Schiela).
Nonlinear dynamics in the quantum world
On smallest scales, nature often behaves very different than human intuition would predict. Investigating dynamical phenomena of the quantum world is an essential ingredient to the understanding of photosynthesis (Kümmel, J. Köhler) or semi-conductors (Axt). Many nonlinear phenomena in the quantum world may be approached via random-matrix theory (Kriecherbauer).
Pattern formation and recognition
Individuals and events follow bio-psycho-social and temporal patterns which can be recognized and classified using nonlinear methods. Such patterns appear in vegetation landscapes (Zimmermann), in talent identification in sport (Hohmann), in geological processes (Keppler) or in mathematical systems such as the Einstein-Vlasov equations (Rein) . On the basis of linear methods alone, such classifications would hardly be successful.
Technological applications
Nonlinearities play their prominent role not only in the natural sciences, but also in technological applications. Examples under investigation in our Focus Area include energy systems (Brüggemann) or material science (Dubrovinskaia). In order to find solutions for such nonlinear systems one requires efficient solution methods (Rauber), optimal control algorithms (Grüne) as well as a deeper understanding of the involved uncertainties (Bebendorf).
